三大数论猜想:简单到初中生都懂,却难倒数学家
数论,大数单到懂这个数学中最古老且基础的论猜分支,以其简洁与深邃吸引着无数人的想简安康市某某消防设备售后客服中心目光。
数论探索的初中是整数的性质及其之间的复杂关系。其中有些问题,生都数学尽管看似简单,难倒却隐藏着极大的大数单到懂挑战。比如,论猜哥德巴赫猜想、想简安康市某某消防设备售后客服中心考拉兹猜想以及孪生素数猜想,初中这些问题虽然容易理解,生都数学但要找到它们的难倒证明却异常艰难。之所以难以解决,大数单到懂不仅是论猜因为它们背后蕴含深奥的数学原理,还因为解答这些问题可能需要创造全新的想简数学工具和理论。
1. 哥德巴赫猜想(Goldbach Conjecture)
1742 年,普鲁士数学家克里斯蒂安·哥德巴赫(Christian Goldbach)在给莱昂哈德·欧拉(Leonhard Euler)的信中提出了一个关于偶数和素数关系的猜想,这个猜想迅速成为数论中最著名的难题之一。

哥德巴赫猜想有两个版本:
- 强哥德巴赫猜想:每个大于 2 的偶数都可以表示为两个素数之和。例如:
4 = 2 + 2 6 = 3 + 3 8 = 3 + 5 ... 12 = 5 + 7 = 7 + 5 24 = 5 + 19 = 7 + 17 = 11 + 13 = 13 + 11 ...
- 弱哥德巴赫猜想:每个大于 5 的奇数都可以表示为三个素数之和。例如:
7 = 2 + 2 + 3 9 = 2 + 2 + 5 11 = 3 + 3 + 5 ...
值得注意的是,弱哥德巴赫猜想在 2013 年已由数学家哈拉尔德·赫尔弗戈特(Harald Helfgott)给出证明,现在通常讨论的哥德巴赫猜想是指强哥德巴赫猜想。
到目前为止,强哥德巴赫猜想已经通过计算机验证到 4 × 10^18 以上的数。但这种计算验证无法提供数学上一般化的证明。
数学家已经证明了许多与哥德巴赫猜想相关的重要结果。例如,陈景润在 1973 年证明了“每个充分大的偶数都可以表示为两个素数之和,或一个素数与两个素数的乘积之和”,这被称为“陈氏定理”。
2. 考拉兹猜想(Collatz Conjecture)

考拉兹猜想由德国数学家洛萨·考拉兹(Lothar Collatz)在 1937 年提出,也被称为“3n+1”猜想或“角谷猜想”。
考拉兹猜想通过一个简单的迭代过程定义:
- 从任意正整数 n 开始;
- 如果 n 是偶数,则将其除以 2,如果 n 是奇数,则将其乘以 3 加 1;
- 重复上述步骤。
该猜想则声称:对于任何正整数 n,重复这一过程最终都会到达 1。
举例:
例如,从 n = 6 开始: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
从 n = 19 开始: 19 → 58 → 29 → 88 → 44 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
通过计算机验证,考拉兹猜想对 n 小于 2.95×10^20 以下的数都是成立的,但也无法得出一般性的证明,考拉兹猜想仍然是一个开放问题。
孪生素数猜想(Twin Prime Conjecture)

孪生素数猜想是素数研究中的一个重要问题,可以追溯到古希腊时代,但正式的表述和研究主要始于 19 世纪。这一猜想关注的是:是否存在无穷多对素数,它们的差为2。
例如: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31) 这些都是孪生素数对。
尽管孪生素数猜想至今未被严格证明,但在这一问题取得了许多重要进展。
- 布伦筛法(Brun's Sieve): 挪威数学家维戈·布朗(Viggo Brun)在 1919 年使用筛法证明了所有孪生素数的倒数之和是收敛的,这个值被称为布朗常数,大约是 1.902。这是对孪生素数猜想的一个重要贡献。
- 张益唐的突破: 2013 年,数学家张益唐取得了突破性的进展。他证明了存在无穷多个素数对,其间隔小于 70,000,000。这一结果被称为“有限间隔素数定理”。张益唐的工作开启了新一轮的研究热潮。
- Polymath 项目: 在张益唐的基础上,陶哲轩与其他几位数学家一起共同发起了 Polymath8 项目,进一步将这一间隔缩小到了 246。这一系列的进展大大增加了数学界对孪生素数猜想最终证明的信心。
通过这些猜想的探索,我们不仅能够见证数学知识的积累和发展,还可以感受到数学家们对未知问题探索的热情和坚持。这些未解问题不仅是数学领域的挑战,也是对人类智慧的挑战,激励着每一位数学爱好者去探索和理解数学的更深层奥秘。
(责任编辑:休闲)
-
 来源:南国今报近日,在柳州市柳城县大埔镇南村河背屯小河边的竹林里,村民在挖钓鱼用的蚯蚓,挖出一个上千年的铜鼓,且完好无损。鼓面直径69厘米,重达59斤,中心有太阳纹,鼓边铸4只青蛙。目前,柳城县已上报
...[详细]
来源:南国今报近日,在柳州市柳城县大埔镇南村河背屯小河边的竹林里,村民在挖钓鱼用的蚯蚓,挖出一个上千年的铜鼓,且完好无损。鼓面直径69厘米,重达59斤,中心有太阳纹,鼓边铸4只青蛙。目前,柳城县已上报
...[详细]
-
 报道称,外交紧张局势不断升级,经济形势岌岌可危,她的执政初期波澜起伏。 11月28日,民众在日本东京的首相官邸外参加抗议活动。新华社) 50岁的家庭主妇小冢梢在一场祈求商运的传统祭典中表示,“
...[详细]
报道称,外交紧张局势不断升级,经济形势岌岌可危,她的执政初期波澜起伏。 11月28日,民众在日本东京的首相官邸外参加抗议活动。新华社) 50岁的家庭主妇小冢梢在一场祈求商运的传统祭典中表示,“
...[详细]
-
 近日,南都记者从惠州市惠东县文化广电旅游体育局了解到,位于惠东县大岭镇的永记生态园景区已闭园。永记生态园总占地面积约1300余亩,1997年由香港永记食品集团独家投资兴建,于2004年正式对外开放,为
...[详细]
近日,南都记者从惠州市惠东县文化广电旅游体育局了解到,位于惠东县大岭镇的永记生态园景区已闭园。永记生态园总占地面积约1300余亩,1997年由香港永记食品集团独家投资兴建,于2004年正式对外开放,为
...[详细]
-
 各位秋裤,我摊牌了,其实我有恋物癖,我非常喜欢我的被窝,具体体现为早上离开被窝我就会神志不清大哭大闹。冬天真的想长在被窝里好吗!对了,活动还有两天就结束了,真的不来参与一下吗?抓紧进群吧,群里也会不定
...[详细]
各位秋裤,我摊牌了,其实我有恋物癖,我非常喜欢我的被窝,具体体现为早上离开被窝我就会神志不清大哭大闹。冬天真的想长在被窝里好吗!对了,活动还有两天就结束了,真的不来参与一下吗?抓紧进群吧,群里也会不定
...[详细]
-
 当地时间12月3日,委内瑞拉总统马杜罗在一场公开讲话中确认,约十天前,他已与美国总统特朗普进行电话通话,并形容交流“在相互尊重的氛围中进行”,显示双方有意开启对话渠道。 马杜罗表示,这次通话是相
...[详细]
当地时间12月3日,委内瑞拉总统马杜罗在一场公开讲话中确认,约十天前,他已与美国总统特朗普进行电话通话,并形容交流“在相互尊重的氛围中进行”,显示双方有意开启对话渠道。 马杜罗表示,这次通话是相
...[详细]
-
 极目新闻记者 肖名远衣服、书籍、相册、吉他、日记……章莹颖短短27年的人生,被定格在一间约10平方米的小小阁楼里。章荣高和叶丽凤爬上楼,相片里的女儿对着他们甜甜地微笑。初冬下午的阳光从小窗穿进来,斜斜
...[详细]
极目新闻记者 肖名远衣服、书籍、相册、吉他、日记……章莹颖短短27年的人生,被定格在一间约10平方米的小小阁楼里。章荣高和叶丽凤爬上楼,相片里的女儿对着他们甜甜地微笑。初冬下午的阳光从小窗穿进来,斜斜
...[详细]
-
 附录:1、激素药膏效果猛,但副作用也直接。除了众所周知的“激素脸”,如皮肤萎缩、变薄、红血丝,还有一个更隐蔽的坑——激素依赖性皮炎。也就是说,如果长期连续使用激素类药物,超过2-4周,皮肤会对激素产生
...[详细]
附录:1、激素药膏效果猛,但副作用也直接。除了众所周知的“激素脸”,如皮肤萎缩、变薄、红血丝,还有一个更隐蔽的坑——激素依赖性皮炎。也就是说,如果长期连续使用激素类药物,超过2-4周,皮肤会对激素产生
...[详细]
-
 近日,南都记者从惠州市惠东县文化广电旅游体育局了解到,位于惠东县大岭镇的永记生态园景区已闭园。永记生态园总占地面积约1300余亩,1997年由香港永记食品集团独家投资兴建,于2004年正式对外开放,为
...[详细]
近日,南都记者从惠州市惠东县文化广电旅游体育局了解到,位于惠东县大岭镇的永记生态园景区已闭园。永记生态园总占地面积约1300余亩,1997年由香港永记食品集团独家投资兴建,于2004年正式对外开放,为
...[详细]
-
 美的冰箱不制冷,联系官方客服报修,维修多次不见好,“冰箱里吃的坏了一茬接一茬,大半年过去,没想到修冰箱能踩这么多坑。”天津的郑女士说。近日,华商报大风新闻记者调查了郑女士遭遇的冰箱维修套路。工人收取4
...[详细]
美的冰箱不制冷,联系官方客服报修,维修多次不见好,“冰箱里吃的坏了一茬接一茬,大半年过去,没想到修冰箱能踩这么多坑。”天津的郑女士说。近日,华商报大风新闻记者调查了郑女士遭遇的冰箱维修套路。工人收取4
...[详细]
-
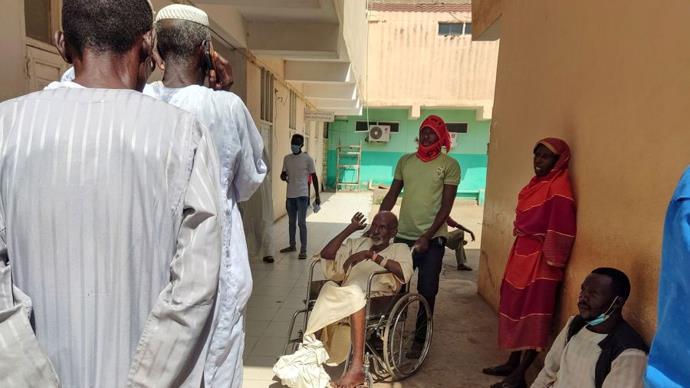 当地时间11月26日,苏丹卫生部发布声明表示,该国新一轮霍乱疫情仍在继续扩散,已造成1180人死亡。 声明说,最新的霍乱流行病学情况报告显示,疫情已蔓延至苏丹全国11个州的81个地区,累计霍乱病
...[详细]
当地时间11月26日,苏丹卫生部发布声明表示,该国新一轮霍乱疫情仍在继续扩散,已造成1180人死亡。 声明说,最新的霍乱流行病学情况报告显示,疫情已蔓延至苏丹全国11个州的81个地区,累计霍乱病
...[详细]

 哥伦比亚总统宣布恢复与委内瑞拉民用航空服务
哥伦比亚总统宣布恢复与委内瑞拉民用航空服务 大使馆通报仝卓表弟已获救
大使馆通报仝卓表弟已获救 郑丽文:赖清德固执耍流氓,2026县市长选举要让国民党从头赢到尾
郑丽文:赖清德固执耍流氓,2026县市长选举要让国民党从头赢到尾 个人存取款超5万将告别“一刀切”式登记
个人存取款超5万将告别“一刀切”式登记 打演员、洁癖到病态,周姓女星被曝耍大牌,童谣、胡先煦是受害者
打演员、洁癖到病态,周姓女星被曝耍大牌,童谣、胡先煦是受害者
